Solving hyperchaotic initial value problems using second derivative extended trapezoidal rule of the second kind blended with generalized backward differentiation formulae with variable step size
Keywords:
SDBETR2s blended with GBDF, Variable stepsize, Hyperchaotic IVPsAbstract
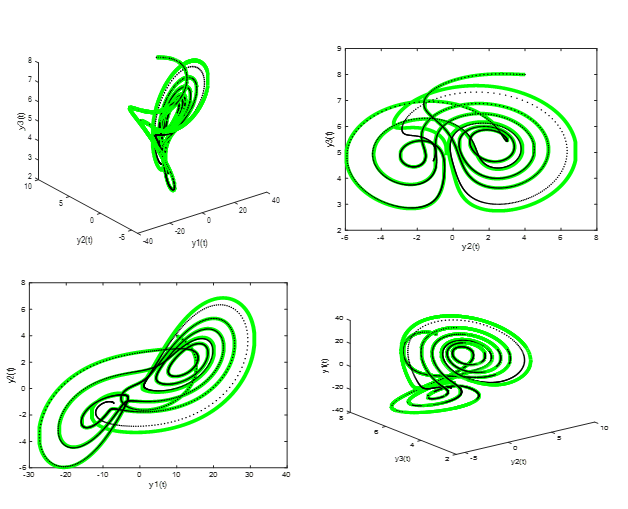
This paper aims to evaluate the accuracy and performance of the second derivative block extended trapezoidal rule of the second kind, blended with generalized backward differentiation formulae using variable step sizes, in solving hyperchaotic initial value problems. Hyperchaotic systems, known for their rapidly changing solutions and extreme sensitivity to initial conditions, pose significant challenges for numerical methods. Traditional approaches often involve linearizing the systems or solving them in multiple sub-intervals, followed by combining the results. However, these methods can introduce errors due to the subdivision of intervals. The proposed method, which integrates the second derivative block extended trapezoidal rule with generalized backward differentiation formulae, offers a more precise solution by eliminating the need for interval subdivision and direct linearization. The continuous formulation of this method is derived using a multistep inversion technique that blends two linear multistep methods, while the discrete schemes are deduced from their continuous interpolants. Convergence analyses of these schemes are presented, demonstrating the efficiency and accuracy of the proposed block methods. As a result, these methods are well-suited for solving hyperchaotic and other nonlinear ordinary differential equations.
Published
How to Cite
Issue
Section
Copyright (c) 2024 E. J. Onoja, U. W. Sirisena

This work is licensed under a Creative Commons Attribution 4.0 International License.







